3.2 Formas geométricas tridimensionales (Superficies planas y curvas).

MÉTODO DE TRASLACIÓN

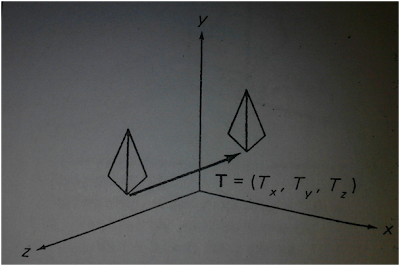
En una representación coordenada homogénea tridimensional, un punto es trasladado (fig.11.1) de la posición (x,y,z) a la posición  (x’,y’,z’) con la Operación matricial.

[x´,y´,z´,1]=[x, y, z, 1]

         

Los parámetros Tx, Ty, Tz, que especifican distancias de traslación para las coordenadas, reciben la asignación  de cualquier valor real. La representación matricial de la ecuación 11.1 es equivalente a las tres ecuaciones

        x’ =x + Tx,   y’ = y + Ty,  z’ =z + Tz

Un objetivo se traslada en tres dimensiones transformando cada punto definidor del objeto. La traslación de un objeto representada como un conjunto de superficies poligonales se efectúa trasladando los valores coordenados para cada vértice de cada superficie. El conjunto de posiciones coordenadas trasladadas de los vértices define entonces la nueva posición del objeto.

MÉTODO DE ESCALACIÓN

Operación matricial.

 [x´,y´,z´,1]=[x, y, z, 1]  

Los parámetros de escalación Sx,  Sy,  Sz, se les asigna asignación cualquier valor positivo.

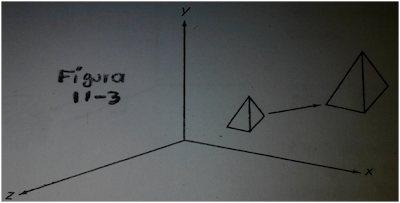
Cuando la transformación 11-3 se aplica para definir puntos en un objeto, el objeto se escala y se desplaza en relación con el origen coordenado. 

MÉTODO DE ROTACIÓN

Para especificar una transformación de rotación de un objeto, se debe designar un eje de rotación (en torno al cual se hará girar el objeto) y la cantidad de rotación angular. En aplicaciones bidimensionales, el eje de rotación siempre es perpendicular al plano xy. En tres dimensiones, un eje de rotación puede tener cualquier orientación espacial.los ejes de rotación más fáciles de manejar son aquellos que son paralelos a los ejes coordenados. Asimismo, podemos valernos de las rotaciones en torno a los tres ejes coordenados con el fin de producir una rotación en torno a cualquier eje de rotación especificado en forma arbitraria.

Las direcciones de rotación positivas en torno a los ejes coordenados son en sentido contrario al del reloj, como se observa a lo largo de la posición positiva de cada eje en dirección del origen.

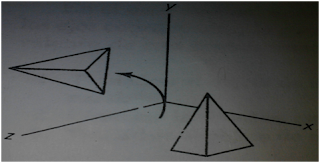
Operación matricial de rotación en el eje Z

El parámetro Ѳ especifica el ángulo de rotación.

[x´,y´,z´,1]=[x, y, z, 1]

Imagen que muestra la rotación de un objeto en torno al eje Z.

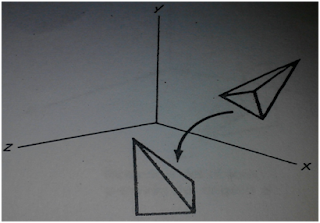
Operación matricial de rotación en el eje X

[x´,y´,z´,1]=[x, y, z, 1]

  

Operación matricial de rotación en el eje y

[x´,y´,z´,1]=[x, y, z, 1]

  

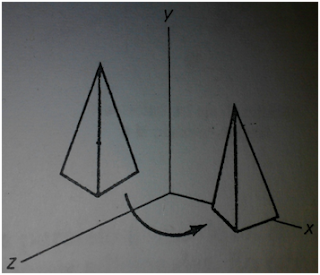
REPRESENTACIÓN EN UN GRÁFICA 3D DE LOS TRES MÉTODOS ANTERIORES:

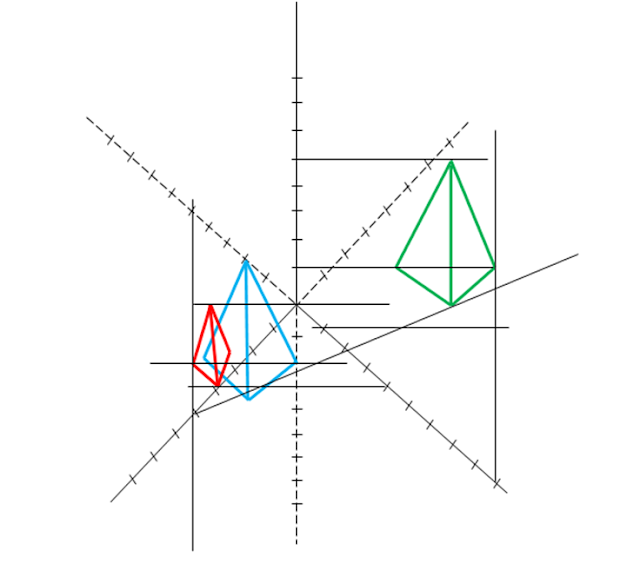
3.4 Lineas y superficies curvas

Las representaciones de líneas y superficies son de aplicación a los procesos de diseño de formas y de desarrollo de planos constructivos. A los tradicionales puntos de vista de si debe determinarse la enseñanza para todas las aplicaciones o por el contrario si debe consistir en una formación de gran contenido geométrico-proyectivo se une la utilización de ordenadores. Para conjugar estas tendencias el autor expone la representación de curvas y superficies de aplicación técnica: Punto, recta, plano, circunferencia, otras curvas planas, hélice cilíndrica, poliedros regulares, superficies radiadas, esfera, etc. El estudio de algunas superficies como las desarrollables, muy importantes en los trazados de construcción naval. Finalmente analiza las ecuaciones analíticas, absolutamente imprescindibles para su representación por ordenador. 

Los métodos más eficientes para determinar la visibilidad de objetos con superficies curvas son la proyección de rayos y los métodos basados en árbol octal. Con la proyección de rayos, calculamos las intersecciones entre los rayos y las superficies y localizamos la distancia de intersección más pequeña a lo largo del trayecto del rayo. Con los arboles octales, simplemente exploramos los nodos de adelante hacia atrás para localizar los valores de color de superficie. Una vez definida una representación en árbol octal a partir de las definiciones de entrada de los objetos, todas las superficies visibles se identifican con el mismo tipo de procesamiento.

No es necesario realizar ningún tipo especial de consideración para diferentes tipos de superficies, ya sean curvas o de cualquier otra clase. Una superficie curva también puede aproximarse mediante una malla poligonal, y entonces podemos utilizar algunos de los métodos de identificación de superficies visibles previamente expuestos. Pero para algunos objetos, como las esferas, puede que sea más eficiente, además de mas preciso utilizar el método de proyección de rayos y las ecuaciones que describen la superficie curva. 

Representación de superficies curvas Podemos representar una superficie como una ecuación implícita de la forma 

f(x,y,z)=0 

o con una representación perimétrica. Las superficies de tipo spline, por ejemplo, se suelen describir mediantemente ecuaciones para métricas. 

En algunos casos, resulta útil obtener una ecuación explicita de la superficie, como por ejemplo una ecuación que nos de la altura con respecto a un plano de tierra xy: Z=f(x,y) Muchos objetos de interés, como las esferas, elipsoides, cilindros y conos tienen representación mediante ecuaciones cuadráticas. 

Estas superficies se suelen utilizar comúnmente para modelar estructuras moleculares, cojinetes, anillos y ejes. Los algoritmos de líneas de barrido y de proyección de rayos requieren a menudo técnicas de aproximación numérica para resolver la ecuación de la superficie en el punto de intersección con una línea de barrido o con un rayo de un pixel. Se han desarrollado diversas técnicas, incluyendo cálculos en paralelo e implementaciones hardware de gran velocidad, para resolver las ecuaciones de intersección con superficies curvas para los objetos más comúnmente utilizados.